There are different kinds of modulation technique based on varying the properties of a pulse train. The Pulse Width Modulation (PWM) varies the width of individual pulses according to the amplitude of the modulating signal. The Pulse Position Modulation (PPM) varies the position of individual pulses from their mean position according to the amplitude of the modulating signal. The PWM is a kind of modulation technique indented for power efficiency, but the power required to transmit individual pulses varies significantly. In PPM modulation technique the power required for transmitting individual pulses are constant, but synchronization of transmitter and receiver are required. There is a simple pulse modulation technique called Pulse Amplitude Modulation (PAM) which is proved to be more power efficient than the PWM and consumes constant power for individual pulses.
In PAM the amplitude of the individual pulses are varied according to the amplitude of the modulating signals. The PAM modulator and demodulator circuits simple compared to other kind of modulation and demodulation techniques. There are two kinds of PAM one in which the pulses have the same polarity and the other in which the pulses can have both positive and negative polarity according to the amplitude of the modulating signal.
This article demonstrate how to generate a single polarity PAM wave corresponding to a modulating sine wave with the help of simplest possible circuitry.
DESCRIPTION:
Unlike the AM modulation which varies the amplitude of the carrier signal in both the sides from the mean position, the PAM modulation varies the amplitude of the pulses only at a single side. Simply the top of the pulses are modulated corresponding to the message signal. In this project the PAM is generated from a pure sine wave modulating signal and a square wave generator which produce the carrier pulses and a PAM modulator circuit. The block diagram of the PAM modulation is given in the following:
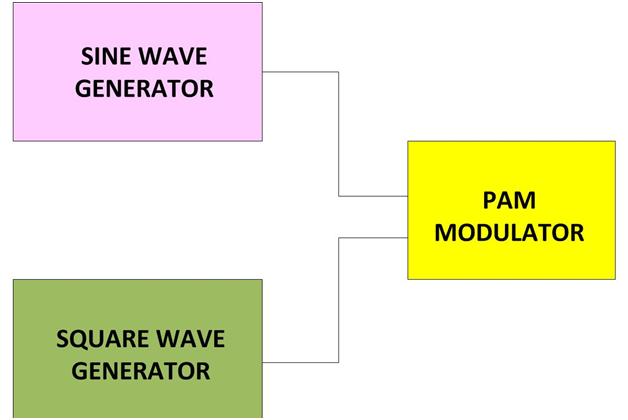
Fig. 1: Block Diagram of Pulse Amplitude Modulation (PAM )
{ 1) Variable frequency sine wave generator
A sine wave generator circuit is used in this project which is based on the Wien Bridge Oscillator (WBO) circuit. The Wien Bridge oscillator circuit can produce distortion less sinusoidal sweep at its output. The circuit is designed in such a way that both the amplitude and frequency of the oscillator can be adjusted using potentiometers.
The circuit diagram of the variable frequency sine wave oscillator is shown in the following:
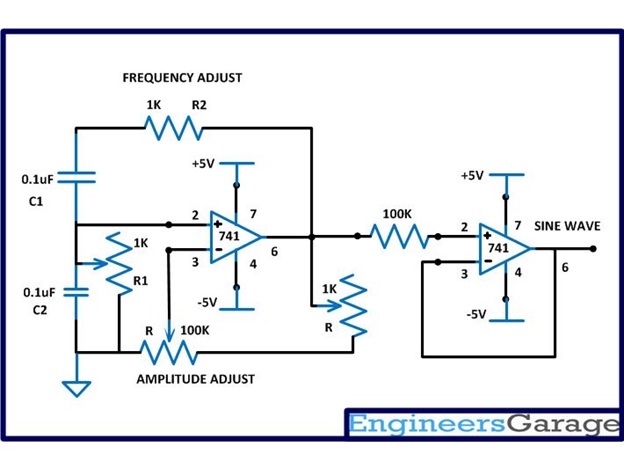
Fig. 2: Circuit Diagram of Variable Frequency Sine Wave Oscillator

Fig. 3: Variable Frequency Sine Wave Oscillator Circuit on Breadboard
The frequency of the above circuit can be varied by simply varying the potentiometer R2 and the amplitude of the wave form can be adjusted by varying the potentiometer R. The frequency of the sine wave generated by the above circuit depends on the components R1, R2, C1 and C2 and the equation for the frequency is given below:
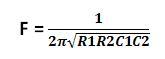
For the ease of adjusting the amplitude of the wave to obtain proper sinusoidal sweep, a coarse and fine adjustment has been implemented using potentiometers. A low value (1K) potentiometer is connected in series with the high value (100K) potentiometer so that the coarse adjustment can be done with the high value resistor and the fine adjustment with the low value resistor.
The snapshot of the waveform formed at the CRO screen using the WBO circuit is shown in the following image:
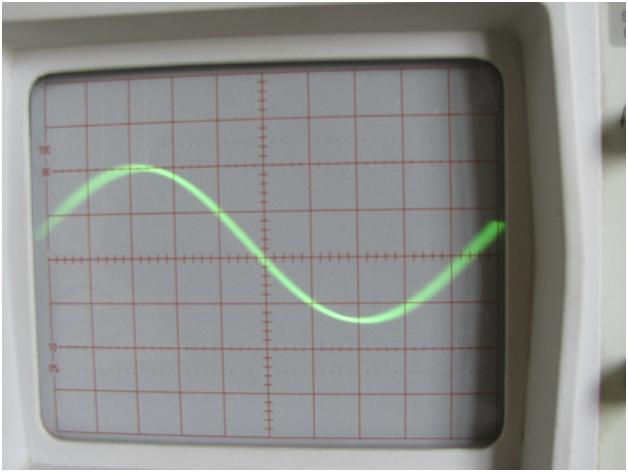
Fig. 4: Sine Wave Waveform Displayed on CRO
{ 2) SQUARE WAVE GENERATOR
The square wave is generated in this project using an op-amp based astable circuit. The op-amp based astable circuit is used to generate the square wave due to the less number of components required and less complex circuit. The ON-time and the OFF-time of the pulses can be made identical and the frequency can be easily adjusted without changing them. However in this project the circuit is designed to be producing a constant frequency. The astable multivibrator circuit using op-amp 741 is given below.
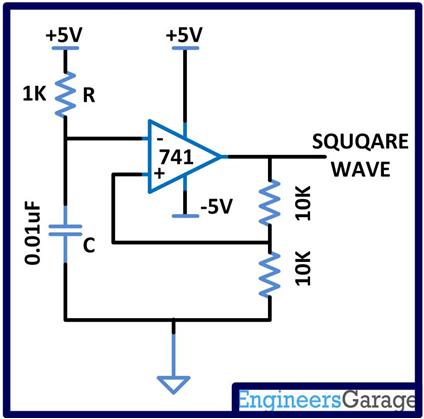
Fig. 5: Circuit Diagram of Square Wave Generator
The time period of the pulses generated by the above circuit depends upon the values of the resistor R and the capacitor C. The following equation gives the approximate time period of the pulses generated by the op-amp astable multivibrator circuit.
T = 2.2 * R*C
PAM Modulator
Since the value of the resistor is selected as 1K and the capacitor is selected as 0.01uF, the time period of the pulse is:
T = 2.2 * 10^3 * 0.01 * 10^-6 = 2.2 * 10 ^ -5 seconds.
Since frequency F = 1 / T, the frequency of the pulses generated by the above circuit is calculated as
F = 1 / 2.2 * 10 ^ -5 = 45 KHz.

Fig. 6: Square Wave Generator Circuit on Breadboard
3) PAM MODULATOR
The PAM modulator circuit in this project has to modify the amplitude of the pulses having a frequency of 45 KHz with the modulating sine wave of frequency 1 KHz. The modulator here is realized using a simple FET and a couple of resistors. The FET used here is BFW10 which is an N-channel FET and since it is a unipolar device it is suitable for applications in which the signals having both positive and negative polarities are used.
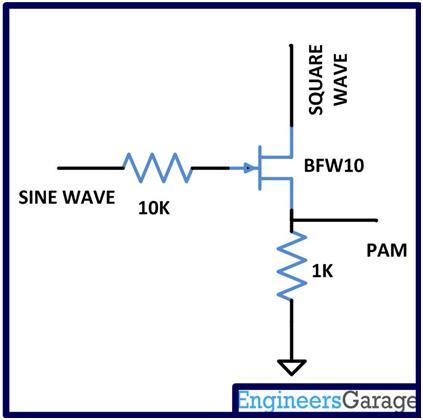
Fig. 7: PAM Modulator Circuit Diagram

Fig. 8: PAM Modulator Circuit on Breadboard
The resistors are simply used as current limiters where the 10K resistor is used to limit the current flowing into the base of the FET and the 1K resistor is used to limit the current flowing through the N-channel. The PAM signal is obtained across the 1K resistor and the ground.
The image of the CRO screen displaying a single polarity PAM wave is given below:
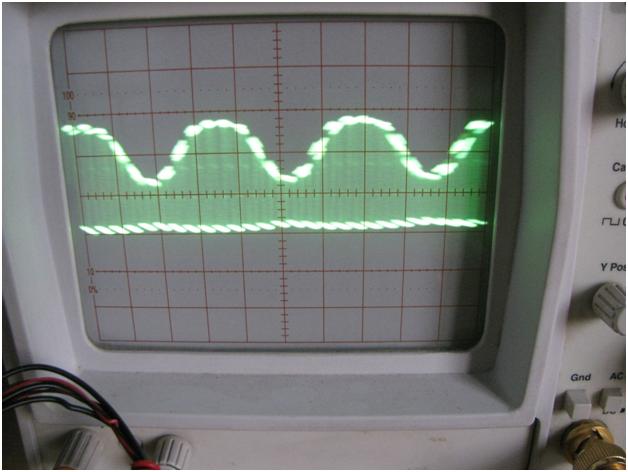
Fig. 9: CRO Screen Displaying Single Polarity PAM Wave
The complete circuit diagram is given below:
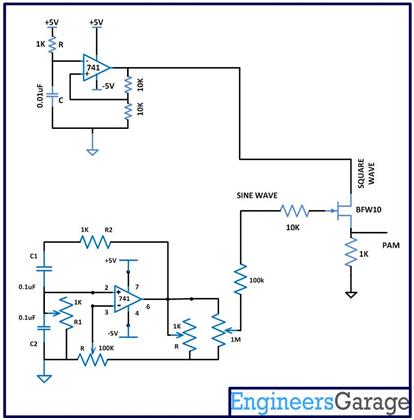
Fig. 10: Circuit Diagram of PAM Modulator
The image of the complete circuit diagram wired in the breadboard is given below:

Fig. 11: Pulse Amplitude Modulation Circuit on Breadboard
Filed Under: Circuit Design


Questions related to this article?
👉Ask and discuss on EDAboard.com and Electro-Tech-Online.com forums.
Tell Us What You Think!!
You must be logged in to post a comment.