Most of the people have noticed a change in the voice of others when they speak through the telephone. Most of the people might have experienced difficulty in hearing other sound in the environment where the person at the other end of the telephone calls from. It happens mostly for high frequency sound like instrument music, sound from video game etc. People who are interested in electronics and who have done some audio circuits with loudspeakers might have experienced an exactly opposite phenomenon in which the sound reproduced by the loudspeaker is more clear and loud for higher frequencies. Also those who have experienced quality of music played through the home theater system know how far better it is from a single speaker which can create the same loudness.The explanation for all the above mentioned phenomenon is simply due to the fact that a simple sound generating device cannot produce all the audible frequencies with the same loudness.
The audible range for human being starts from 20Hz to 20 KHz and it varies from person to person and significantly with the increasing age of each one. The voiced speech of a typical adult male will have a fundamental frequency from 85 to 180 Hz, and that of a typical adult female from 165 to 255 Hz. The telephone can reproduce the sound which falls in the range of 300 Hz to 3 KHz only. It is only due to the presence of higher harmonics of the human voice in that range makes the telephone useful. Since the maximum frequency is only 3 KHz the higher frequency sounds are little audible through the telephone.
The telephone system is only an example which has been optimized to perform at a certain range of frequency. Such a kind of optimization is required in most of systems because when it comes to the electronic devices like filters, amplifiers, loudspeakers etc. their characteristics vary with frequency of operation. This change in characteristics with the frequency explains why the home theaters with different kind of loudspeakers are able to produce high quality sound including all the high frequency and low frequency sounds which are not at all possible with a single loudspeaker.
The mechanical construction of the loudspeaker plays a significant role in deciding its performance at different frequency range but those who are designing circuit for the loudspeaker are more interested in an important electrical characteristic of the loudspeaker called impedance. This article discusses how to measure the impedance of a loudspeaker at a required frequency of operation.
DESCRIPTION:
Every electronic component including resistors, capacitors and inductors produce a resistance to the current flowing through it and it is generally called impedance irrespective of the component. This impedance value for a particular device may or may not vary with the frequency of the current flowing through it. A good quality resistor has almost the same impedance value from 0 Hz (DC) frequency to infinite hertz, but the impedance of a capacitor decreases with frequency and an inductor increases with frequency. Thus in case of a resistor the resistance and the impedance has the same value. Simply the impedance is the resistance of any component at a given frequency and hence impedance value of a component isalso represented in Ohms. Like the resistance is denoted with letter ‘R’, the impedance is denoted with the letter ‘Z’.
The impedance of a loudspeaker has very high variations with the frequency of operation and it is significant in the design of audio devices like amplifiers, speaker drivers etc. Consider the case of an amplifier with a loudspeaker at its output.
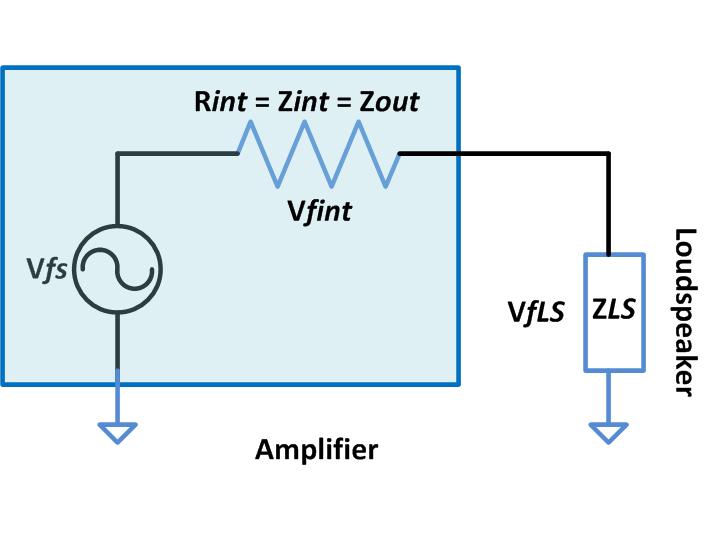
Fig. 1: Circuit Diagram Of Amplifier With Loudspeaker at Output
The amplifier is a device which can source a current to the loudspeaker and every current sourcing device has an internal resistance and here it is represented as a resistance Rint. Since the resistor has the same value for its resistance and impedance it is also marked as Zint. This internal resistance of the amplifier is also referred to as the output resistance and hence it is marked as Zout. The impedance of the loudspeaker is represented as Zls.
In the above system both the Zout and Zls comes in series with each other and the same current flows through both of them. As in the case of a two resistors connected in series with each other, the same current flowing through two impedances connected in series will generate different voltages across both the impedances. In the above figure Vfsis the voltage of the fictional source inside the amplifier which is generating the frequency and the Vfintis the voltage drop across the internal resistance and the Vflsis the drop across the loudspeaker.
From the above figure it can be understood that even though the amplifier generates a voltage Vfsthe loudspeaker receives only a voltage of Vflsand the rest will get dropped across the internal resistance as given by the following equation:
Vfint= Vfs–Vfls
The value of the voltage drop by the same current across the impedances depends upon the value of the impedance and the value of the current flowing through them. If the voltage at the operating frequency is represented by ‘Vf’ and the current by ‘If’and the impedance by ‘Z’, the Vfis directly proportional to the Z as given by the following equation:
Vf= If * Z
Applying this knowledge in the above equation it can be re-written as the following:
Vfint= Vfs– If * Zls
From the above equation it is clear that the loudspeaker with low impedance ‘Zls’will produce large internal voltage drop ‘Vfint’ in the amplifier and vice versa. Since the impedance is frequency dependent one should find the loudspeaker which provides the highest impedance at the operating frequency. The variation of the impedance of a common loudspeaker can be plotted as shown in the following figure:
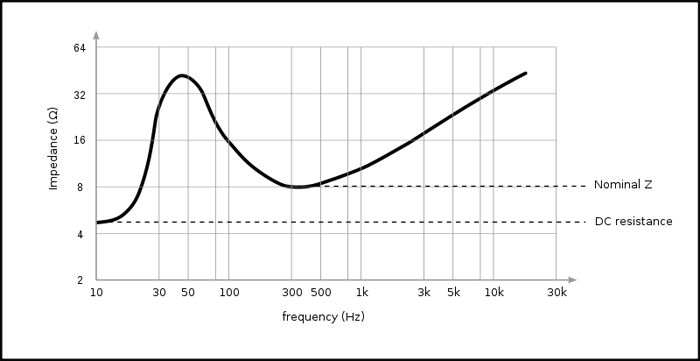
Fig. 2: Variation Of Impedance in Loudspeaker Represented Through Graph
The direct method to calculate the impedance of a loudspeaker at the required operating frequency is to connect it with a pure sine wave generator having the frequency same as the required operating frequency and measure the voltage drop across the loudspeaker. The details of the sine wave generating circuit used to calculate the impedance of a loudspeaker is discussed below. Since in audio applications the impedance should be calculated for a range of frequencies and hence a variable frequency sine wave generator has been designed based of Wien Bridge oscillator.
Variable frequency sine wave generator
Variable frequency sine wave generator
The sine wave generation circuit used in this project is the Wien bridge oscillator circuit. This is the only circuit which can generate the pure sine wave without any distortion. The amplifier component used in the Wien bridge circuit is an op-amp with dual-power supply. Both the circuits are built around the versatile op-amp IC, 741. The circuit of the sine wave generator is shown in the following figure.

Fig. 3: Circuit Diagram Of Sine Wave Generator
The frequency of the above circuit can be varied by simply varying the potentiometer R2 and the amplitude of the wave form can be adjusted by varying the potentiometer R. The frequency of the sine wave generated by the above circuit depends on the components R1, R2, C1 and C2 and the equation for the frequency is given below:
For the ease of adjusting the amplitude of the wave to obtain proper sinusoidal sweep, a coarse and fine adjustment has been implemented using potentiometers. A low value (1K) potentiometer is connected in series with the high value (100K) potentiometer so that the coarse adjustment can be done with the high value resistor and the fine adjustment with the low value resistor.
Another important modification done in the circuit is that a buffer has been added at the output end of the oscillator. This will help to prevent the loading effect of the loudspeaker on the oscillator circuit. The modified circuit diagram with the coarse and fine adjustment and the buffer implemented is shown in the following figure:
Fig. 4: Circuit Diagram Of Sine Wave Generator With Buffer
Fig. 5: Sine Wave Generator With Buffer Circuit On Breadboard
Calculating the impedance
The sine wave generator is connected to the loudspeaker through a small valued resistor and in this method the impedance is calculated after measuring the voltage across the loudspeaker and the voltage across the resistor. The connection of the circuit is represented using the following block diagram:
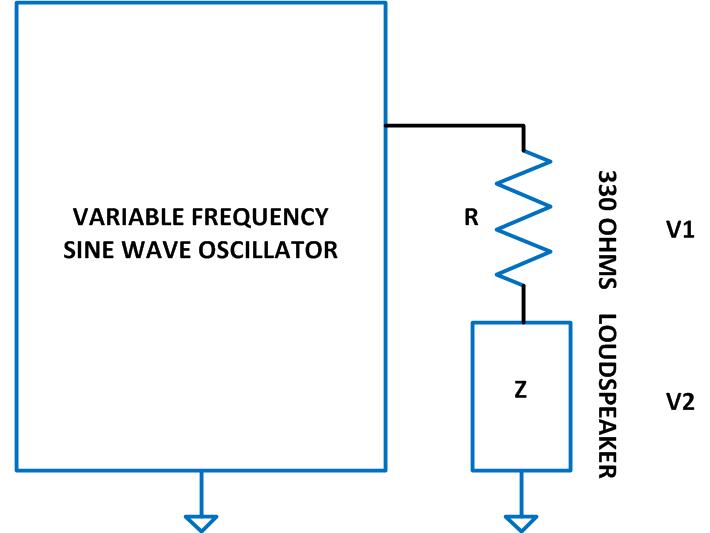
Fig. 6: Block Diagram Of Sine Wave Generator Connected to Loudspeaker through Resistor
The impedance of the loudspeaker ‘Z’ can be calculated using the following relation:
Z = V2 R/ V1
Impedance Calculation
The circuit diagram and the images of the circuit are shown in the following figures:
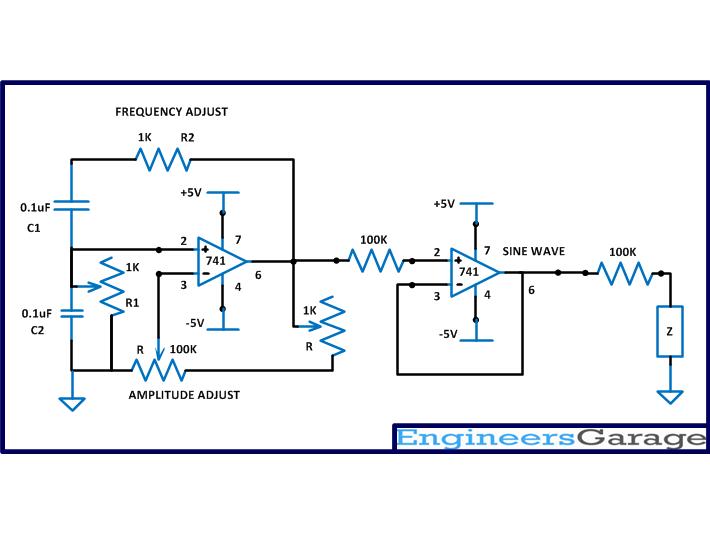
Fig. 7: Circuit Diagram Of Sine Wave Generator With Loudspeaker
Calculating the impedance of a loudspeaker for an operating frequency of 1 KHz is discussed in the following:
The frequency applied is a pure sine wave of frequency 1KHz as shown in the following image.
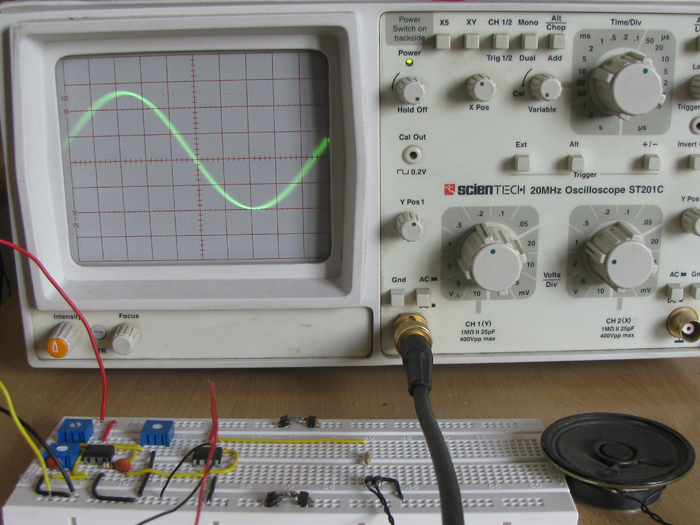
Fig. 8: Sine Waveform with Opposite Polarity Generated on CRO
The amplitude is calculated using the CRO and is found to be 4.2 Vp-p.
The waveform that appears across the loudspeaker appears as shown in the following figure:
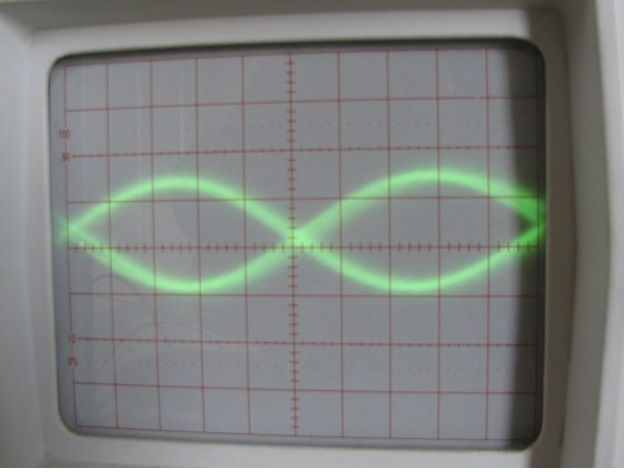
Fig. 9: Sine Waveform with exactly opposite in phases Generated on CRO
The two sine waves which are exactly opposite in phases can be seen and one of them is the original sine wave applied and the other is the reflected sine wave from the loudspeaker due to the inductive impedance. This reflected wave should be eliminated using proper impedance matching circuit: otherwise it will affect the proper functioning of circuits like amplifiers or oscillators where the loudspeaker is connected to.
Here the voltage drop across the loudspeaker is measured as 0.12 Vp-p. Hence the V2 is 0.12 Vp-p and the V1 can be calculated as 4.2 – 0.12 Vp-p.
Now applying these values on the equation and the impedance can be calculated for 1 KHz sine wave as given below:
Z = (0.12 * 330) / (4.2 – 0.12)
This will give a value of 9.7 ohms, slightly above the nominal value (8 ohms) of the loudspeaker used here. Using the same method the impedance is calculated for 200 Hz as 8.46 ohms which is very close to the nominal value of 8 ohms. The impedance calculated is found to be almost double the nominal value for a sine wave of 20 KHz.
For generating the higher frequency sine wave using the Wien bridge oscillator circuit one can simply replace the value of capacitors to 0.01uF.
For a loudspeaker the impedance in the audible frequency range is always equal to higher than the nominal impedance value. One can use this method to calculate the impedance of any loudspeaker at the frequency of operation and can design the impedance matching circuits or amplifier circuits accordingly.
Filed Under: Circuit Design


Questions related to this article?
👉Ask and discuss on EDAboard.com and Electro-Tech-Online.com forums.
Tell Us What You Think!!
You must be logged in to post a comment.