The main function of filters is to suppress or filter out components from mixed frequency signals for clear communication. As we learned in the first article of this series, filters permit a range of frequency to pass that’s known as “pass bend,” rejecting (or suppressing) other frequencies known as “stop bend.”

The cut-off frequency is the parameter that separates these two bends. Depending on the pass and stop bends, there are four types of filters: Active low-pass, high-pass, band-pass, and band-reject filters.

In this tutorial, we’ll cover the band-pass filter (BPF), which allows the pass band of frequencies between the higher and lower cut-off frequencies.

There are two cut-off frequencies for the BPF:

1. The upper cut-off frequency (f1): a frequency below where all other frequencies are passed

2. The lower cut-off frequency (f2): all of the frequencies above this frequency are passed

From this f1 and f2, let’s  define the following parameters, which represent the designing parameters for the BPF.

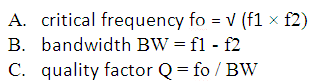
The listing of the different parameters for a band-pass filter.

Based on “Q,” we have two types of band-pass filters…

1. A wide band-pass filter: with Q <10, it has a wide flat response over a range of frequencies. The BW is also greater.

2. A narrow band-pass filter: with Q>10, it has a sharp bell-type of response. In this case, the BW is much lower.

The wide band-pass filter
The wide BPF is a combination of the LPF and HPF as shown here:

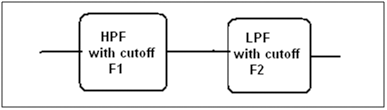
An overview of the wide band-pass filter.

Here, F2 > F1. This means that we have to design the HPF with F1 and LPF with F2. Now, let’s suppose we want to pass the band of frequencies between 2 to 5 kHz. so F1 = 5000 Hz and F2 = 2000 Hz.

Designing the HPF section

• Step 1: First, assume the required value of the capacitor. It should be less than 0.1 micro Farad. This is necessary for better frequency stability. Let’s assume the value C as the 10 nF (nano farad).
• Step 2: Calculate the value of the resistance from the equation.

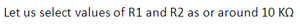
The calculations required to find the resistance of the HPF in a wide band-pass filter.

Our assumption for the capacitance value as 10 nF is good (or, at least, OK). If we calculate the value of R it’s much less than 1 KOhm. So, we have to assume some other value for the capacitor because the value of R should not be less than 1 K Ohm.

• Step 3: Next, choose the required pass-band gain. Let’s use 2 for this tutorial.

Here’s the equation…

Af = 1 + (R2 / R1)

2 = 1 + (R2 / R1)

R2 / R1 = 1

R2 = R1

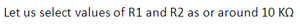
The calculations required to find the resistance of the HPF in a wide band-pass filter.

Designing the LPF section

• Step 4: Now, assume the required value of the capacitor. Let’s suppose we assume the same value C as for10 nF.
• Step 5: Calculate the value of the resistance from the equation.

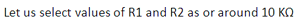
The calculations required to find the resistance of the LPF in a wide-band pass filter.

This value is an odd one for the resistor and may not be available as a fixed value. We might be able to use the potentiometer of 4.7 and tune it to the desired value.

• Step 6: Choose the required pass-band gain. If we use 2 again, then…

R2 = R1

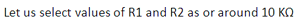
The calculations required to find the resistance of the LPF in a wide band-pass filter.

The final design with the component values is shown here. The op-amp is an active component and it requires +ve and -ve biasing voltages. It’s possible to test the circuit by applying input through the signal generator and observing output on the DSO or oscilloscope and the bode plotter.

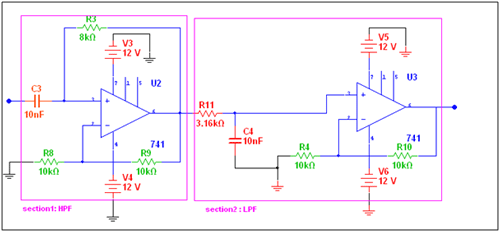
A circuit diagram of the LM741 OPAMP IC-based wide band-pass filter.

Note: I have simulated the above circuit in NI’s multisim 11 software. The schematic design is also prepared using the same software. The software is available as a free one-month trial period from National Instrument’s (NI) website. The below circuits are also prepared using the multisim 11 software and tested in it.

The narrow band-pass filter 

• Step 1: For simplicity, let’s assume C1 = C2 = C
• Step 2: Select the centre frequency, FC = 2 KHz, with a pass-band gain of Af = 2, and Q = 10
• Step 3: Next, assume the capacitor value C as 100nF
• Step 4: Calculate the value of the R1 from

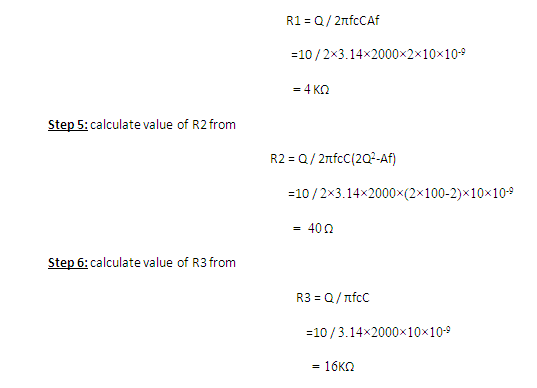
The calculations required to find the resistance for the narrow band-pass filter.

Here’s the final design:

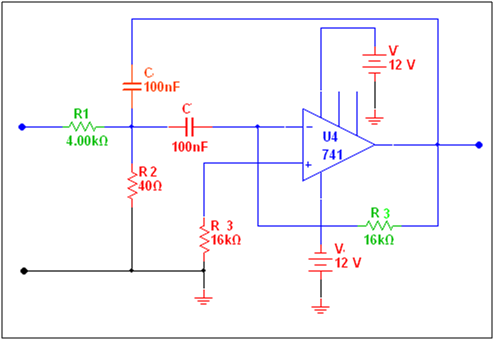
The circuit diagram of the LM741 OPAMP IC-based, narrow band-pass filter.

 

 

---

Filed Under: Tutorials

 

---

---

---