Pulse code modulation is a form of information conversion from discrete to digital. Pulse code modulation is used in almost all modern communication systems and is essential for digital communication. Each sampled value is given in the form of a discrete signal, converted to its binary equivalent, and coded in the form of zeros and ones. There are different types of pulses used for coding ones and zeros. In the following program the user is asked to select the pulse which will then be used to modulate the incoming digital signal.

Working Principle

Each discrete signal consists of a set of values. In order to convert this signal into digital form, each discrete value must be represented as its binary equivalent. This binary number can be of any number of bits, where a greater number of bits means better accuracy, but also increased memory and bandwidth usage. For this project, we use 3 bits which will represent 8 values( from 0 to 7). The only issue is that the values of a discrete signal can be much grater than 7 or much smaller than 1. In this case we have to normalize it. We do this by dividing the entire signal vector by its maximum amplitude, so it can have values ranging only from 0 to 1. We then multiply this by 7 so that it now has values from 0 to 7, as required

Types of Pulses

Three different types of pulses are used in the program , all with their advantages and disadvantages.

Return to zero pulse:

If the pulse has a period of T seconds, for a digital ‘1’ it is on for T/2 seconds and off for T/2 seconds. For a digital ‘0’ it is off for T seconds

Example: for T=30

On:

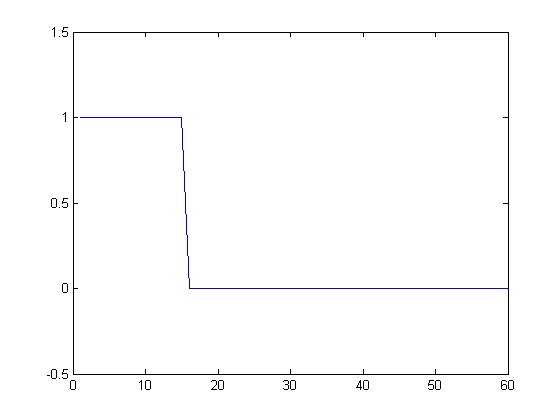
Fig. 1: Signal Diagram showing ON state of Return to Zero Pulse 

Off:

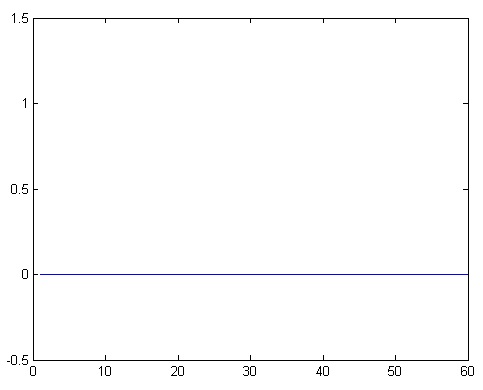
Fig. 2: Signal Diagram showing OFF state of Return to Zero Pulse 

Not Returning to zero (NRZ):

 As the name suggests, this pulse does not return to zero for a digital ‘1’, i.e. for a period of T seconds, it is on for T seconds. For a digital zero it is off for T seconds.

Example : for T=30

On:

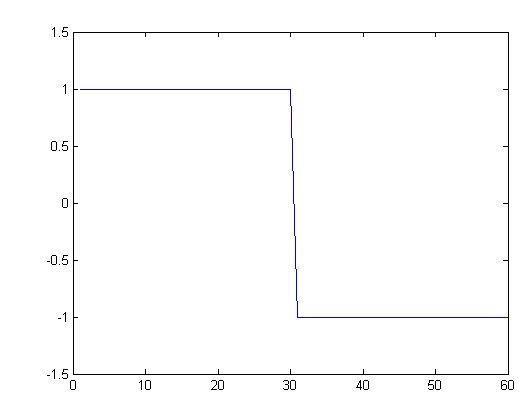
Fig. 3: Signal Diagram showing ON state of Not Return to Zero Pulse 

Off: 

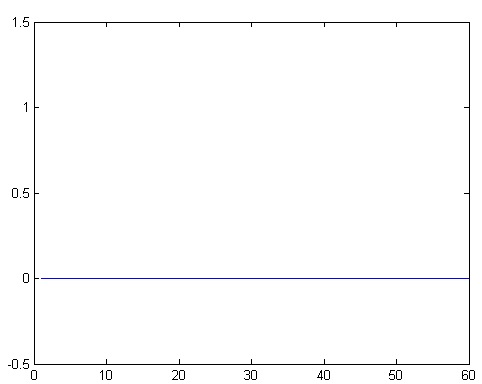
Fig. 4: Signal Diagram showing OFF state of Not Return to Zero Pulse 

Manchester Pulse and Output

Manchester pulse:

This is an alternating type of pulse. For a digital one, the pulse is on for the first T/2 seconds the off for the next T/2 seconds. For a digital zero, the pulse is off for the first T/2 seconds the on for the next T/2 seconds. This pulse has the advantage that there is no DC component present in the modulated signal,  however, it takes up twice the bandwidth of NRZ pulse.

Example: for T=60

On:

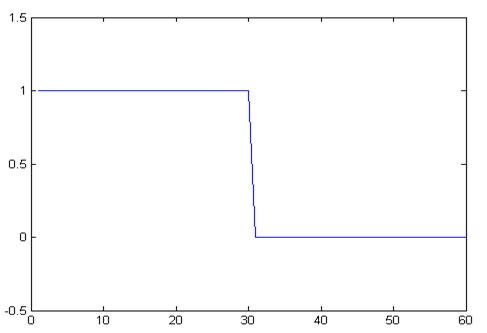
Fig. 5: Signal Diagram showing ON state of Manchester Pulse

Off:

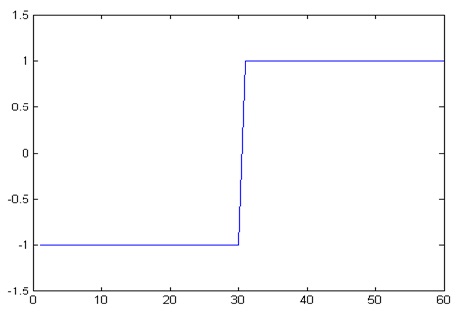
Fig. 6: Signal Diagram showing OFF state of Manchester Pulse

Algorithm and Code explanation

        Step 1 – Clear all existing windows and variables

        Step 2 – Take the input signal from the user and store it in the variable ‘signal’

       Step 3 – The signal has to be normalized. In our program we use 8-bits (values ranging from 0 to )hence our normalized signal is the input signal divided by its maximum and then multiplied by 7

        Step 4 – Define two empty vectors binsignal and pulsesignal to represent the binary value and pulse output of each signal value respectively

        Step 5 – For each value of ‘signal’ obtain its binary value using the dec2bin function

       Step 6 – The binary value is a string. In order to convert it to a matrix of zeros and ones, subtract the ascii value of 0 ie 48 from the binary value and store it in ‘binvalue’

        Step 7 – Concatenate ‘binvalue’ with the existing binsignal and repeat from step 5 until the whole signal is converted into binary values.

        Step 8 – Take input from the user to determine which type of pulse is to be used.

        Step 9 – Define the pulses for RZ, NRZ, and Manchester types.

        Step 10 – Define an empty vector pulsesignal.

        Step 11 – Read ‘binsignal’ for each value of binsignal, concatenate the appropriate pulse with the pulsesignal matrix.

        Step 12 – Plot the output pulsesignal using plot() function.

Output

Fig. 7: Screenshot of Matlab Code for Pulse Width Modulatiin and Line Coding

Fig. 8: Screnshot of Matlab Output for Pulse Width Modulation and Line Coding 

Project Source Code

###


clc; clear all; close all;
signal=input('enter signal');
i=[];
normsignal=(signal./max(signal))*7;
binsignal=[];
pulsesignal=[];
for i=1:length(signal)
    binvalue=dec2bin(signal(i),3);
    binvalue=binvalue-48;
    binsignal=[binsignal binvalue];
end
pulse=input('choose pulse: 1=Return to Zero, 2=Not return to Zero 3=Manchester');
if pulse==1
    for i=1:length(binsignal)
        if binsignal(i)==1
            pulsesignal=[pulsesignal ones(1,10) zeros(1,10)];
        end
        if binsignal(i)==0
            pulsesignal=[pulsesignal zeros(1,20)];
        end
    end
end
if pulse==2
    for i=1:length(binsignal)
        if binsignal(i)==1
            pulsesignal=[pulsesignal ones(1,20)];
        end
        if binsignal(i)==0
            pulsesignal=[pulsesignal zeros(1,20)];
        end
    end
end
if pulse==3
    for i=1:length(binsignal)
        if binsignal(i)==1
            pulsesignal=[pulsesignal ones(1,10) (-1*ones(1,10))];
        end
        if binsignal(i)==0
            pulsesignal=[pulsesignal (-1*ones(1,10)) ones(1,10)];
        end
    end
end
plot(pulsesignal);          
###