What Buddha saw of the world, Matisse sought in his paintings, and Heisenberg found in the quantum, was a simple fact that “Precision is not the truth”. They all found out in different novel ways that things can be a certain degree true, and a certain degree false at the same time. Drawing absolutes can certainly increase precision, but cannot make it perfectly precise as is clear from the finite word length effects in the digital domain. In a quest to seek the ultimate, in a bid to imitate the human capabilities, we have constantly resorted to the continuum of phenomenon and not discreteness. This is the world of fuzzy logic.
History
The roots of Fuzzy Logic date back to the time when intelligent life forms evolved and they all can be classified as fuzzy systems. While Aristotle, presented the system of two valued logic, it was Plato who laid the foundations of what would be known as fuzzy logic by proposing that there was an intermediate third region in between ‘true’ and ‘not true’ where some part might be true, while some part might not be. The subject then never found any mention in history while probability continued to thrive until the early 1900’s when Lukasiewicz proposed the idea of three valued logic True-Possible-False [0, 1, 2].
His student Knuth proposed a different range of values [-1, 0, 1]. For the first time after having being used for centuries in the functioning of the brain, the term was formally introduced by Lotfi A. Zadeh, renowned as the father of fuzzy logic, in 1965. He observed that conventional Two Valued binary logic could not manipulate data with subjective ideas like, fairly cold, or extremely hot. It cannot classify the different shades of gray owing to the two valued nature because of which it either has to be black or white. It was him who introduced the nomenclature and fuzzy set theory with values in between 0 and 1.
While scientists in US did not pay much heed to the concept finding its name child-like, it started gaining grounds in unexpected quarters. E.H. Mamdani, London, built the world’s first fuzzy logic controller to control the speed of a small steam engine and achieved great success. The oriental countries of Japan and China readily accepted the concept and started developing it. While the US were still contemplating over the childishness of the name, Japan built a train controlled by fuzzy logic which is said to have such smooth functions that if one was standing inside one such moving train, he couldn’t tell if the train was moving at all unless he saw the world flashing by in the windows.
Fuzzy Logic can be viewed as a super set of Boolean logic, as a multi-valued logic. It adds degrees between the absolute truth and absolute false to cover partial truth in between. In simple terms, fuzzy logic involves classifying objects and functions into fuzzy sets which could be given linguistic phrases. It is a form of reasoning that is neither exact, nor absolutely inexact. For example, too hot, little slow, phrases which do not give the idea of absolute, but a fuzzy estimate. While 33 degrees might be warm enough for a person from the equator, someone from the arctic might find the heat unbearable, or too hot. It is not possible to classify them into strict sets with defined boundaries which leads to the idea of fuzziness.
It has basically evolved from predicate logic, though many forms called t-norm fuzzy logics do exist in propositional logic too. It generally has an object and a predicate. For example: in the sentence, “Plato is a man”, ‘Plato’ is the object, and “is a man” is the predicate. But an important point about fuzzy logic is that it is deterministic and time-variant. A few salient points explained by Zader Lotfi on fuzzy logic are:
1. Exact reasoning or precise values is the extreme or limiting case of approximate reasoning.
2. Any system which works on logic can be fuzzified and everything would be a matter of degrees.
3. Knowledge is a collection of fuzzy constraints on a group of variables.
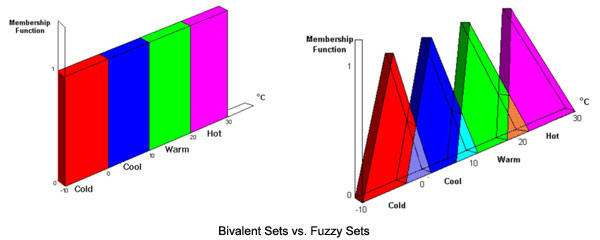
Fig. 1: Image Showing Comparison Between Bivalent And Fuzzy Sets
The bivalent sets being mutually exclusive it is not possible to have membership of more than one set. This leads to ambiguity in reasoning and perceptions as common sense fails to register the hard line rule. The same phenomenon when explained using fuzzy sets grants degrees of membership in the subsets through a membership function. It can help circumvent the rigorous mathematical modeling in system design.
Working
How Fuzzy Logic works can be understood in a simple example of driving in a lane within speed limits. While the driver may take precise inputs (not fuzzy) from the speedometer, he also keeps an eye on the drivers behind him, ahead of him and an overall trend of the speed of the traffic, density pouring in from side lanes etc. to have a rough estimate of conditions. The whole information is processed and summarized into a crisp output of the speed decision he maintains, whether to speed or not. This is a simple example of fuzzy logic.
Like any other mathematical modeling process, FL too uses a few steps to achieve the final goal. The various steps are outlined as:
1. System Requirements: Define control objectives, specifications, criteria, type of response needed, possible failure modes etc.
2. Input/Output relationship: Choosing the minimum number of fuzzy variables for inputs and their relation to the output. These can be linguistic variables, for example for error measurements, large positive error, zero error, small negative error etc.
3. Create FL Membership Functions: These define the values of Input/output terms used in the rules. These represent graphically, the magnitude of participation of an input and associate a weight to each input which determines their influence on the final output. These functions seldom have simple shapes, and may range from triangular to bell shaped, trapezoidal or exponential. The degree of membership is determined by having the input on the x-axis and projecting it to the upper boundary of membership function.
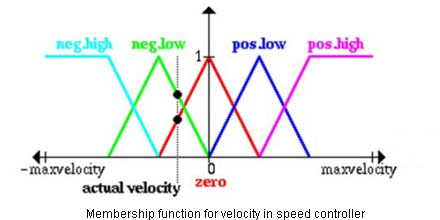
Fig. 2: Graph Showing FL Membership Functions For Velocity In Speed Controller
4. Rule Based Engine Structure: FL systems are based more on intuitive reasoning with If-Then clauses for all the possible cases. There is no Else clause, which means that all the conditions are checked. A rule matrix is initially formed to tabulate all the possible number of rules. Though all might not be needed, it helps mapping out the possible inputs while keeping the system under control.
5. Create Routines: In case of software, pre and post-processing routines, and in hardware programs, putting rules into the FL Engine.
6. Defuzzification: The firing strength of each rule is determined and logical products of each rule are inferred through techniques like max-min’d, root-sum-squared, max-dot’d etc. before passing them to the defuzzification phase. Defuzzification involves the conversion of the fuzzy data into a crisp output using the Fuzzy Centroid Algorithm.
7. Testing and Evaluation: The objective is to try and try again until the goal is achieved. The rules are changed and new rules may be added to tune the system to achieve the desired performance.
Fuzzy logic has always been a controversial subject. Researchers often argue that it is just another way of expressing probability. This however, is not true. While probability is the mathematical modeling of degree of ignorance and deals with the stochastic uncertainty of an event happening or not, Fuzzy logic is the modeling of degree of semblance which expresses the uncertainty of the clear definition of the event itself. While many argue over the similarity of the two subjects, its pioneer Lotfi, argues that both are different and none is the replacement of the other.
There are a few requirements for a Software Development Kit (SDK) to qualify as a good fuzzy logic SDK. Firstly, it should support all the design phases ranging from design to the implementation phase. Secondly, it should support all the targeted platforms and the various industry standard interfaces like DLL/DDE/OLE. The hard way to do it is to use a programming language and do it all manually which is not only exhaustive and tiring, but every minute change in the design would require rewriting the entire code. Since the time of 8 bit MCUs, dedicated hardware for fuzzy systems has been favored because of the advantages involved like reduced processing time.
Hardware & Application
First generation of fuzzy hardware was of analogue type and came from Japan in 1980’s. These processors used fuzzy gates in computation having switching times in nanoseconds with accuracy within 0.1%. However, they never found their way out of the research mainly due to lack of programmability. Second generation was Digital Fuzzy Processors. The name can be considered to be a misnomer as something can either be digital, two valued or fuzzy which is continuous. These digital processors however worked on fuzzy instruction sets utilizing multilayered structure in interfacing.
An interface layer fetched the fuzzy inputs which were then written onto the fuzzy processor via the host MCU communicating with the fuzzy processor through a Dual Port Ram (DPRAM). This however had a disadvantage of increased latency, complexity of code and overhead for communication between the two processors. These successfully made into the market in 1990’s but were soon to be succeeded by the third generation of Integrated Fuzzy Processors. It can be achieved by two techniques, by integrating the two co-processors on the same chip thus increasing the speed and reducing communication overhead. This however leads to increase in chip size.
Another approach is to enhance the existing instruction set. This offers threefold increase in computation of FL while achieving compactation of the code at the same time. The only problem is that this needs the redesigning of the MCU.
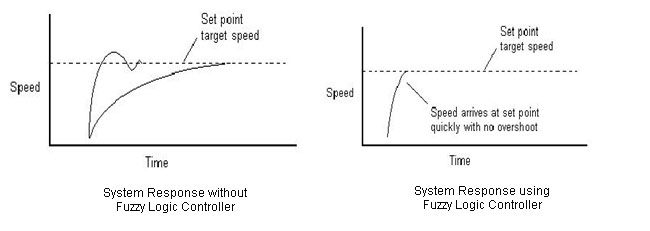
Fig. 3: Typical Linear First Order System Curves Using Conventional Control And Fuzzy Logic
The curves shown above are the typical of a linear first order system using conventional control and fuzzy logic, think of them as speed control system. The improvement of fuzzy system over conventional mathematically modeled system is quite evident in the form of lesser time taken to reach the desired speed and lesser overshoots.
But there is a problem with fuzzy logic when used as a standalone solution. It works by evaluating each and every rule, greater the number of rules, better the system. Further, these rules are predefined making the system data set dependent and non-adaptive. Thus to make these systems more self-reliant, a black box of Neural Networks is put in between the inputs and the fuzzy processor to compute the set of membership functions and constructing the rule matrix. It is this clever combination of the two that leads us to better systems and a new dimension called – Neurofuzzy.
Anti-Lock braking systems that come in most modern cars employ fuzzy systems. Basically fuzzy system can be employed in any control system where fast and tight control is required. Diverse fields ranging from the day to day appliances like an intelligent washing machine which senses the amount of clothes and decides the type of washing, to traffic light control system for increased efficiency in traffic management, to cognitive air conditioning, to sophisticated research fields like language processing and artificial intelligence to industrial applications like robotic control as a replacement for the PID controllers have found usage and wide scale acceptance of Fuzzy Logic.
United Kingdom Transplant Support Service Authority uses FL in prioritizing the kidney waiting list. On the first sight itself, fuzzy logic looks more appealing to a human mind because of the innate similarity in the decision making processes of the brain than any form of two valued logic which always leaves scope for ‘What if’s’. Thus while researchers might still argue that fuzzy logic is just another manifestation of probability or there is nothing fuzzy about fuzzy logic, they sure cannot underrate the advancements that fuzzy logic has helped in achieving.
Filed Under: Articles


Questions related to this article?
👉Ask and discuss on EDAboard.com and Electro-Tech-Online.com forums.
Tell Us What You Think!!
You must be logged in to post a comment.