In embedded systems, a simple function rarely exists alone. A simple pushbutton and LEDs controller is useful but if that controller cannot report when a user has pressed a button or share the status its LED indicate, the controllers are not worth their value. Many embedded systems include peripheral devices connected to the microprocessor in order to expand its capabilities. For example, Ad fruit Motor Shield SPI,L3G4200D 3-Axis Gyro I2C or SPI, 1.44″LCD Display USART, and so on. Data transmission between two these entities plays a major role in designing embedded systems. In general, the medium of data transmission can be either serial or parallel. All these peripheral devices interface with the microcontroller via a serial protocol. Protocol is a language that defines the mode of communication between systems and devices like protocols specify the aspects of inter-device communications including bit ordering, bit pattern meanings, electrical and mechanical aspect. UART, SPI, TWI, or USB are some of the protocols widely used in embedded systems for serial data communication. The key to increase the value is communication on a communication bus of choice for embedded systems of all sizes.
Fig. 1: Overview of I2C Serial Communication
In today’s electronics era, communication with EEPROM, real-time clocks (RTC), displays, sensors, and much more, has become less complex, easier and require less hardware space in electronics design, all these has been possible because of I2C only. Philips Semiconductors (presently, NXP Semiconductors) has developed a two-wire bus protocol for inter-integrated circuit systems in 1982, commonly known as I2C protocol. Different devices can communicate with each other and can exchange their information/data over this bus only.We, especially electronics design engineers have worked with this protocol in most of ourprojects.
A discussion about understanding the I2C protocol would involve a look into the following:
· A Brief aboutI2C Protocol
· Need of I2C Protocol over other protocols
· Digging a little deeper around it
· How does it work?
· More advanced feature using it
· Understand the protocol from developer end
· A general guideline for its protection.
· The drawback of using I2C
The above discussion would need the readers to have a basic understanding about:
– What is the Protocol?
– What is a bit, byte, and frame?
– What is serial communication?
Let’s delveinto some of the basics:
§ A Brief AboutI2C Protocol
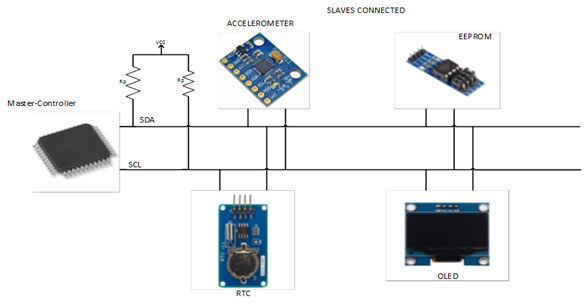
The inter-integrated circuit or I2C Protocol is a way of serial communication between different devices to exchange their data with each other. It is a half-duplex bi-directional two-wire bus system for transmitting and receiving data between masters (M) and slaves (S). These two wires are Serial clock line or SCL and Serial data line or SDA. Masters and Slaves play important role in I2C communication. Master is the one which initiates a communication, generates a clock and terminates the communication and Slave is the one which is handled by master and acts according to the master command. It can also be possible that multiple masters can communicate with multiple slaves. In Figure 2, we can see two Masters are communicating with multiple slaves over I2C Bus.
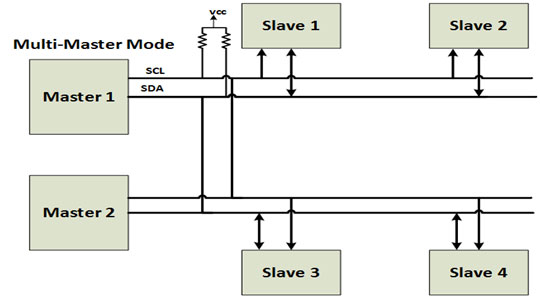
Fig. 2: Overview of Multi-Master Mode of I2C Communication
Each I2C device (Master/slave) is identified by its 7-bit or 10-bit unique address known as device ID which is provided by device manufacturer only and can act as a transmitter or receiver at a time, depending on the configuration of it. As we know, the bus consists of SCL and SDA line, SCL (serial clock line) is responsible for synchronizing the communication and is controlled by Master (the slave can also control the clock line, we will discuss about this topic later) and SDA (serial data line) is responsible for providing the data bi-directionally and can be used by master or slave or both.
There are mainly four modes which define the data rate of the I2C communication system:
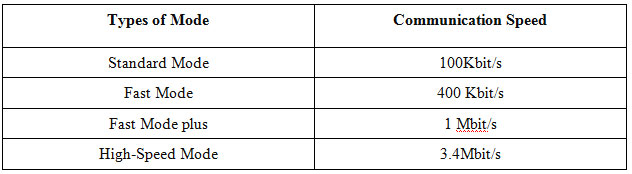
Fig. 3: Table listing various modes of communication of I2C interface and their data transfer rates
We normally work with standard and fast mode for communication.
§ Need of I2C Protocol Over Other Protocols
Before I2C, different devices used to communicate using UART and SPI protocols.A brief about them is as follows:
UART (Universal asynchronous receiver transmitter), as the name indicates, is an asynchronous communication protocol which doesn’t use any clock source for synchronizing the data, so there are more chances of losing the data over UART protocol. The first chip on UART was designed in around 1971. It is one of the simplest forms of data transmission from a controller/PC. It requires a minimum of two pins (transmitter and receiver pin) and a common ground line for data communication. The UART chip is generally found inbuilt in most of the microcontrollers. As only two devices can communicate with each other over a UART bus, it is not well suited for multiple devices communication. The highest data rate UART can support is 230 kbps–460 kbps which was still a low speed as per the requirements.
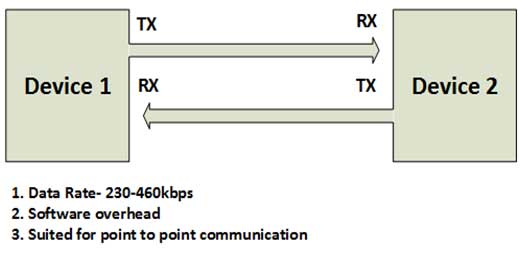
Fig. 4: Overview of UART Serial Communication
SPI (Serial Peripheral Interface) was developed by MOTOROLA and it is very renowned name in data transmission. It has only three lines (i.e. MISO, MOSI, and SCK) for data transmission as well as for handshake unlike UART (which requires 9 pins for full feature operations). In SPI communication there is only one MASTER controller and one SLAVE controller, and hence the slave addressing is not required. It is a full duplex serial data communication process. SPIcan be used for multiple device communication. It is a minimum of 4 wire interface which is a major drawback for today’s electronics demand where everything is going to be in a very compact form. SPI needs 3+n wires i.e. MISO, MOSI, SCK, CSn for every slave connected to the master. If 2 slaves need to be connected then CS pin will be treated individually for every slave device; we will need 5 pins to connect 2 slaves (MISO, MOSI, SCK, CS1, and CS2). It’s a huge loss for a cheap controller which has less number of pins. SPI is a single-master multi-slave protocol, it cannot support multiple masters communicating with multiple slaves.
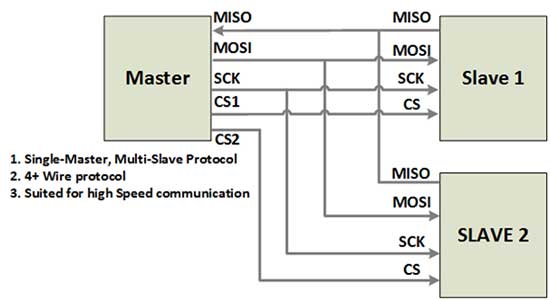
Fig. 5: Overview of SPI Serial Communication
Because of the drawbacks of UART and SPI, there was need of a protocol which can decrease the number of wires required for communication, have flexible data rates along with multiple master and multiple slave communication. This broughtI2Cto the picture which have all the desired features of a multi-bus communication.
§ Digging a Little Deeper Around It
So, we are now clear with our basics of what is I2C and how it differs from other protocols. The TWI/I2C (I-two-C) protocol was invented by Philips. In TWI, the serial data transmission is done in asynchronous mode. This protocol uses only two wires for communicating between two or more ICs. The two bidirectional open drain lines named SDA (Serial Data) and SCL (Serial Clock) with pull up resistors are used for data transfer between devices.Let’s now dig deep around the terms which are going to be used in our further tutorial:
Transmitter and Receiver Device—Transmitter’s (TX) responsibility is to transfer the data and receiver’s (RX) duty is to accept the data from transmitter. Transmitter/receiver can be master or slave or both but one at a time. In the whole tutorial, we will deal with the master, slave, transmitter and receiver. So, we shouldn’t get confused by the use of the term.
Half Duplex Communication—I2C is a half-duplex communication meaning in transmission or reception of data between two devices, only one type of communication can be established at a time. The bus can perform either read or write operation at a single time.
Device Supporton the Bus—According to I2C specs, in 1982, I2C was only allowed for 100KHz data communication with 7-bit addressing i.e. it could support only 112 devices on the bus with 16 reserved addresses. In 1992, it was announced that I2C could support a data rate of 400KHz with 10-bit addressing, this has increased the number of devices support on the bus. 7-bit and 10-bit addressing devices can be connected to the same I2C bus & all devices (7-bit/10-bit) can support all data speed modes. Currently, 10-bit addressing is not much popular in use.
R/ Operation—In master and slave communication, if either of them wants to write, then it needs to send 0 in place of write bit operation in the address frame and if wants to read, then it needs to send 1 in place of reading bit operation in the frame.
Open-collector or open-drain bus—In Figure4, we can see the internal structure of the I2C bus drivers SCL/SDA, consisting of a buffer to read the input and a pull-down (short to GND) FET to transmit the data. A device is only able to pull the bus line to go low in a conductive state; it cannot drive the line high. This is called open-drain or open collector mechanism. Open-drain refers to a type of output at the collector or drain that can drive the corresponding line to go low voltage (generally ground) but cannot drive the line to a high voltage. So, we need to add pull-up resistors on the line so that when drivers are in idle condition, they must not be floating and can restore the signal to default high in the non-conductive state.
Thus, no device may force a high on a line (because the bus lines are active low), this means that the bus will never run into a communication issue where one device may try to transmit a high, and another transmits a low, causing a short (power rail to ground).
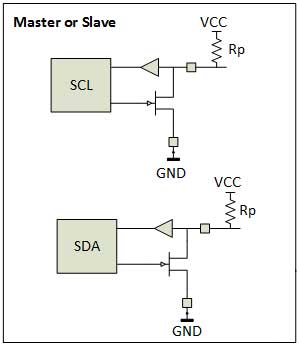
Fig. 6: Circuit diagram of internal structure of I2C Bus Drivers
The value of the pull-up resistors depends on the bus capacitance of the line. In general, we can take a value between 4k7-10k ohm. But to specific, please refer section “Calculation of pull-resistor Rpvalue”.
Data Corruption—I2C doesn’t support push-pull mechanism so no data gets corrupt in the communication process. Because when one master in multi-master environment drives the bus line to go from high to low but when it sees that the line is already low because some other master is using the line, it halts its communication and waits for the completion of the line to go in the idle state. This is another benefit of the I2C protocol.
§ How Does It Work?
This section will take a closer look on how they actually work in a protocol.The TWI or I2C is one of the serial data transfer protocols used in embedded systems. It was created by NXP Semiconductors, originally a Phillips semiconductor division, to attach slow speed peripheral devices to the embedded microprocessor. It is used for low to medium data rate communication. EPROM, real time clock system storage devices, remote temperature sensors and I/O port expanders are some examples of slow peripheral devices. In TWI the serial data transmission is done in asynchronous mode. This protocol uses only two wires for communicating between two or more ICs. I2C is a Multi-point protocol in which a maximum up-to 128 peripheral devices can be connected to communicate along the serial interface which is composed of a bi-directional line (SDA) and a bi-directional serial clock (SCL). The two bidirectional open drain lines named SDA (Serial Data) and SCL (Serial Clock) with pull up resistors. The bus consists of just two wires or circuit traces, one for clock and the other for data, with a pull-up resistor on each wire of the bus. One of the two devices, which control the whole process, is known as Master and the other which responds to the queries of master is known as Slave device. The ACK (acknowledgement) signal is sent/received from both the sides after every transfer and hence reduces the error. SCL is the clock line bus used for synchronization and is controlled by the master. SDA is known as the data transfer bus. Figure below shows a typical arrangement of I2C.
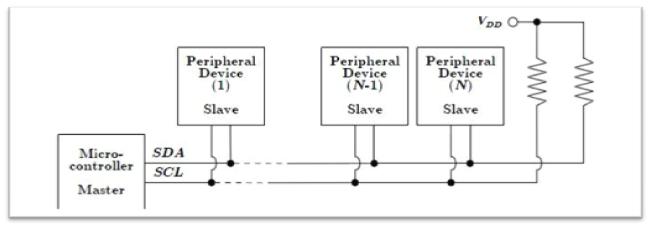
Fig. 7: Image showing peripheral devices connected to Master device over I2C interface
Once we have understood the basics of TWI let’s get in depth about each part of I2C arrangement and functions.
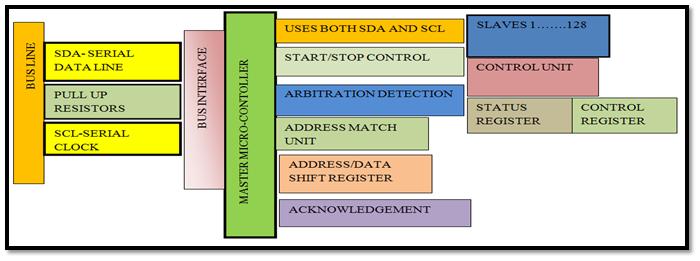
Fig. 8: Image showing building blocks of I2C Serial Interface
Working of TWI
Working of TWO wired interface:
Both TWI lines SDA and SDC are bi-directional therefore outputs connected to the TWI are open collector type so each line is connected to a voltage supply via Pull up resistor. Pulling the lines to the ground is considered a logical zero while letting it float is considered as logical ‘1’. When idle, both lines are high. To start a transaction, SDA is pulled low while SCL remains high. Releasing SDA to float high again would be a stop marker, signaling the end of a bus transaction.
The only external hardware needed to implement the bus is a single pull-up resistor for each of the TWI bus lines. All devices connected to the bus have unique address. The TWI bus is a multi-master bus where one or more devices, capable of taking control of the bus, can be connected. The master supplies the clock; it initiates and terminates transactions and the intended slave (based upon the address provided by the master) acknowledges the master by driving or releasing the bus. The slave cannot terminate the transaction but can indicate a desire to stop or terminate by a “NAK” or not-acknowledge. Addressing opens the lines of communication between the master and its intended slave device and the master keeps the connection open until it wishes to terminate the connection (when the master is finished with the slave).
The mode of operation whether a device will act as a master or as a slave is distinguished by the TWI status codes in the TWI Status Register (TWSR) and by the use of certain bits in the TWI Control Register (TWCR). The status codes are divided in Master and Slave codes and further in receive and transmit related codes. Status codes for Bus Error and Idle also exist. The status codes are divided into four groups: Master Transmitter Mode (MT), Master Receiver Mode (MR), Slave Transmitter Mode (ST) and Slave Receiver Mode (SR).
Once decided which device will act as master the data transmission takes place. Only Master devices can drive both the SCL and SDA lines while a Slave device is only allowed to issue data on the SDA line. Data transfer is always initiated by a Bus Master device.
A high to low transition on the SDA line while SCL is high is defined to be a START condition or a repeated start condition.
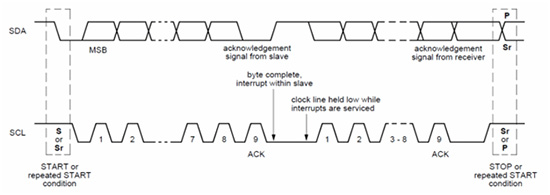
Fig. 9: Signal Diagram for Start Condition of I2C Communication
A START condition is always followed by the (unique) 7-bit slave addresses and then by a Data Direction bit. The Slave device addressed now acknowledges to the Master by holding SDA low for one clock cycle. If the Master does not receive any acknowledgement the transfer is terminated. Depending of the Data Direction bit, the Master or Slave now transmits 8-bit of data on the SDA line. The receiving device then acknowledges the data. Multiple bytes can be transferred in one direction before a repeated START or a STOP condition is issued by the Master. The transfer is terminated when the Master issues a STOP condition. A STOP condition is defined by a low to high transition on the SDA line while the SCL is high. If a Slave device cannot handle incoming data until it has performed some other function, it can hold SCL low to force the Master into a wait-state. All data packets transmitted on the TWI bus are 9 bits long, consisting of one data byte and an acknowledge bit. The master or the control unit includes the clock, Data/Address Register, a START and STOP controller and arbitration detection while the receiver is responsible for acknowledging the reception. The Address Match unit is only used in slave mode, and checks if the received address bytes match the 7-bit address in the TWI Address Register (TWAR). Upon an address match, the Control Unit is informed, allowing correct action to be taken. An Acknowledge (ACK) is signaled by the receiver pulling the SDA line low during the SCL cycle. If the receiver leaves the SDA line high, a NACK is signaled. During data transfer the two wire data register contains the address or data bytes to be transmitted or received. In addition it also contains a register containing the ACK/NON-ACK bit to be transmitted or received.
The START/STOP Controller is responsible for generation and detection of START, REPEATED START, and STOP conditions. The START/STOP controller is able to detect START and STOP conditions even when the MCU is in one of the sleep modes, enabling the MCU to wake up if addressed by a Master. If the TWI has initiated a transmission as Master, the Arbitration Detection hardware continuously monitors the transmission trying to determine if arbitration is in process by synchronizing with Address match unit. Arbitration is a technique which allows to ensure that no two microcontrollers tries to send data at the same time. If the TWI has lost arbitration, the Control Unit is informed. Correct action can then be taken and appropriate status codes generated.
As the TWI bus is a multi master bus, it’s possible that two devices initiate a transfer at the exact same time. Arbitration is carried out through the next stages of the transaction, and the first device attempting to transmit a logical ‘1’ while another device transmits ‘0’ will lose arbitration. This can due to the physical characteristics of the bus easily be detected. If one device pulls a line low, the others cannot transmit high. When a device has lost arbitration, it must stop transmitting and wait until the next STOP condition before trying to take control of the bus again.
TIMING DIAGRAM
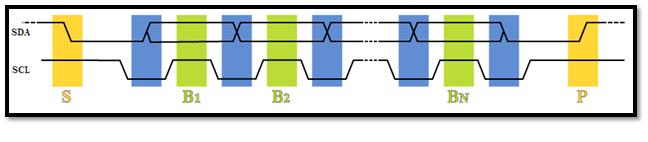
Fig. 10: Timing Diagram of I2C Communication
Data transfer is initiated with the START bit (S) when SDA is pulled low while SCL stays high. Then, SDA sets the transferred bit while SCL is low (blue) and the data is sampled (received) when SCL rises (green). When the transfer is complete, a STOP bit (P) is sent by releasing the data line to allow it to be pulled up while SCL is constantly high. In order to avoid false marker detection, the level on SDA is changed on the negative edge and is captured on the positive edge of SCL.
TWI Details
TWI (Two Wire Interface) Details:
TWI (Two wire interface) as the name suggests is based on two wires namely SDA (Serial Data) and SCL (Serial Clock). The master controls the two buses and slave always responds to the master’s queries. There can be multi master or single master mode of communication. The article Using I2C in AVR ATmega32 shows the communication between two ATmega32 controllers single master mode.
The master initiates the communication by sending a Start condition on the SDA and SCL line. A high to low transmission on SDA line while SCL is high is defined as a Start condition.
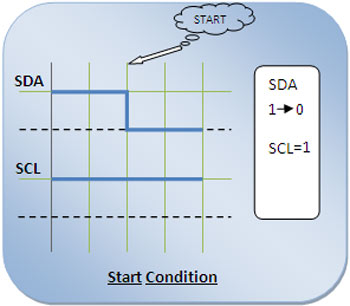
Fig. 11: Signal Diagram for Start Condition of I2C Communication
In return the master updates its status values. The status values are the predefined values and cover the different states that the TWI can be in after every operation of data transfer. Error detection or the faulty transmission can be detected by looking at the status values. The status values are determined by using TWSR register for AVR microcontroller (refer ATmega32 TWI registers).
The start condition is followed by seven bit slave address and then by a data direction bits. Every slave is recognized by its address (The slave address is assigned to slave device at the time of slave initialization). The Data Direction Bit tells the direction of data flow. If the data direction bit is logic zero the master performs write operation with slave or if the data direction bit is logic one then the master performs read operation from slave. The data direction bit is also known as Read/Write Control bit.

Fig. 12: Image showing typical data format of start condition of I2C Communication
If a particular slave device is addressed, the slave acknowledges to master by holding SDA low for one clock cycle.

Fig. 13: Image showing data format of start condition of I2C Communication addressing specific Slave Device
Depending on the DDB (data direction bit) the master or slave transmits the data (8-bit data) on SDA pin. Receiving device then acknowledges the data. The acknowledgement signal updates the status register.

Fig. 14: Image showing typical data format of I2C Communication for transfering a single byte
When data transmission is completed the Stop Condition is issued by master to stop the communication. A low to high transmission on SDA line while SCL is high is defined as a Stop condition.
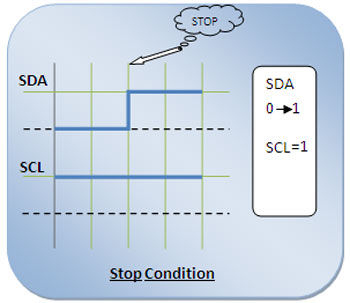
Fig.15: Signal Diagram for Stop Condition of I2C Communication
Note: Multiple bytes can be sent in one direction without repeated start or stop condition.

Fig. 16: Image showing typical data format of I2C Communication for transfering multiple bytes
AVR (ATmega32) contains some in built registers which not only reduce the level of complexity but also make the whole communication process smooth. There are various stages in completing the communication between master and slave devices. Here, we are taking Microcontroller as a Master and peripherals like EEPROM, RTC etc. are slaves. And we are taking 7-bit addresses space for the slaves.
There are basically two operations involved in the communication process:
1. Transmission of data from Master to Slave
2. Reception of data from Slave to Master
E.g. I2C displays are the example in which master transmits the data to the slave to display it on the screen. Temperature or motion sensors are the example where master takes the required data from the slave and process it. EEPROM is the clear example which shows transmission and reception i.e. bi-directional data communication between Master and slave to write and read the data in memory locations.
Note: Below, We will talk about the addresses of the device. For better understanding, we can take any I2C device (e.g. BMA250) and go through the datasheet. Because datasheet says everything about the slave address, register/data address etc.
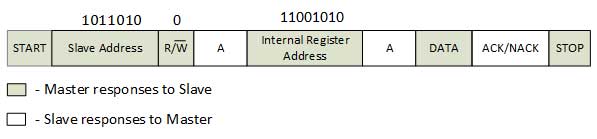
Steps involve for writing the data from Master to Slave: Address- 1011010, Register Address – 11001010
1. To start communication, Master first sends a START command to the bus.
2. Then sends the 7-bit unique address of the desired slave with the write operation command set to 0.
3. Wait for the acknowledgement (ACK) from the slave/receiver.
4. All connected slaves listen to the address and matched slave responses with ACK byte set.
5. For successful acknowledgement, it sends the required internal 8-bit register address of the slave to which data needs to be written.
6. The selected slave matches the register address, If matches, sends the ACK bit to set otherwise, it sends NACK byte (Non-Acknowledgement byte, describe later.)
7. Master again waits for the acknowledgement.
8. For successful acknowledgement, write the 8-bit data to the slave. When complete data is written on the slave, Slave sends an acknowledgement bit ACK to the Master to notify that it is the end of the writing process.
9. The Master then sends a STOP command as a termination signal to the bus.
And this process goes on until Master writes the complete data to the slave.
And the process goes on until the Master reads the complete data from the slave.

Fig. 18: Image showing data format for Master Device reading from Slave Device
§ Discuss in detail about the frame structure:
START and STOP Command—In the I2C protocol, we know that the communication is initiated by the Master, the master sends a START condition. And is terminated by the Master itself only, it sends a STOP condition to end the communication process. To send a START byte, the master sends a HIGH to LOW transition signal at SDA line while leaves the SCL remains in the HIGH state only. If in the multi-master communication protocol, if two or more masters wishes to send START byte on the I2C bus, then whoever sends the HIGH-to-LOW transition first at the SDA line, takes part in communication process first.
And to send a STOP byte, Master sends a LOW to HIGH transition signal at SDA line while leaves the SCL remains in the HIGH state. From this, it is indicated to all slaves that the communication process is ended now.
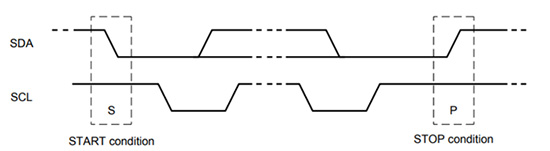
Fig. 19: Signal Diagram for Start and Stop Conditions of I2C Communication
Repeated START condition—The Repeated START condition is very similar to the START condition just a difference of “without terminating the communication with STOP condition”. This is used when a master wants to write multiple data to the device without ending the communication. In this case, the master sends back to back start condition with the necessary addresses to take or provide the data from/to the slave and in the end, sends STOP condition.
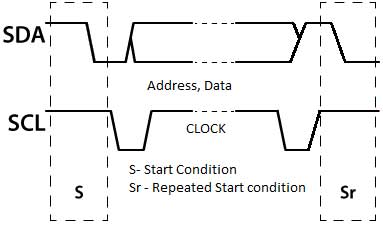
Fig. 20: Signal Diagram for repeated Start Condition of I2C Communication
Data Stability—The state change of bytes in SDA line only takes place when SCL line goes LOW to avoid the false START and STOP condition. When SCL line goes HIGH, the SDA line state needs to be in a stable state only (Whatever state it is in).
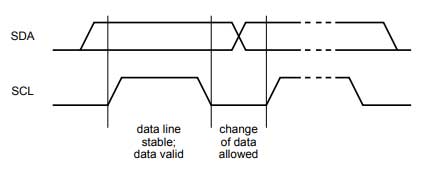
Fig. 21: Signal Diagram showing data validity conditions
Device Address Frame—We know that Every device is identified with its unique 7-bit or 10-bit address. After sending the START byte, the master sends the desired slave address to which it wishes to communicate. In a multi-slave environment, the slave with the matched address will listen to it and will acknowledge to the master. With the address frame, Master sends another bit called read or write bit. If Master wants to write the data on the slave, it sends the slave address (start with MSB) followed by 0 byte. If the master wants to read the data from the slave, it sends the slave address followed by 1 byte.
Acknowledgement and Not-Acknowledgment byte—If a master writes something to the slave, for successful writing, the slave responds with a successful acknowledgement. If the slave writes something to master, then master responds with successful acknowledgement byte to the slave. This applies to every frame (data, register, address) in the I2C bus communication.
Before the receiver sends an acknowledgement byte, the transmitter releases the SDA line free; now if the receiver pulls the SDA line low during the low phase of the clock and if SDA remains stable low during the high phase of the clock, the transmitter gets a successful acknowledgement.
If the receiver does not pull the SDA line low during the low phase of the clock, it remains high or changing during the acknowledgement clock period or high clock period, the transmitter assumes it as a Not-acknowledgement byte. And there are various reasons for the NACK byte:
– The receiver is busy doing some process so it is not able to send the ACK byte.
– The receiver is not able to understand the data from the transmitter and doesn’t send any ACK byte.
– No receiver is present at that moment or receiver is damaged during the process.
– Master-receiver notifies the slave-transmitter for the end of the data transfer.

Fig. 22: Signal Diagram of Acknowledgement byte Response in I2C Communication
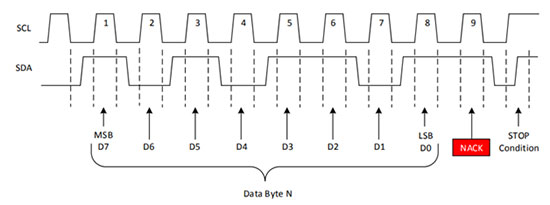
Fig. 23: Signal Diagram of Not-Acknowledgement byte Response in I2C Communication
Register Address Frame—sIf the master wants to write some data to a slave or if it wants to read the data from the slave, the slave devices (e.g. BMA250) have particular 8-bit internal registers to read the data. By sending the internal register address, the receiver (Master) can fetch the data from the transmitter (Slave). The master continues to generate the clock through SCL line and sends the internal register address via SDA line and if the address is valid, the master gets an ACK byte to 1 otherwise 0.
Data Byte Frame—The data byte frame is 8-bit long and this frame data depends on the read or write operation bit sent by the master. If it is a read operation bit, then after successful acknowledgement receives from the slave, the master is ready to read the data from the slave. If it is a write bit, then Master is ready to write the data on the slave.
The number of data frames is arbitrary meaning n number of frames can be read or write, and most slave devices auto-increments the internal register address for the subsequent read or write operation. So, overall this is how I2C works for read and write operation. For more details to implement, refer Section“Understand the protocol from developer end”.
§ More Advanced Feature Using It
We’ve studied regarding the basic operation and working of I2C, this time, we will look over some advanced topics which are useful while handling I2C communication in a precise way.
10-bit addressing Devices—To increase the number of supported devices for the I2C bus, Philips introduces a 10-bit addressing system. This system is very similar to the 7-bit addressing system. We’ve already studied the 7-bit addressing space earlier so, understanding this will be easy for us.
In 10-bit addressing, two address frames are required to transmit the slave address. The first frame consists of “11110ab” where first 5 bits are constant and other 2 bits vary with the slave MSBs address, “a” represents the 9th bit of 10-bit slave address and “b” represents the 8th bit of the slave address. And, the second frame represents the other 8 bits (7th – 0th bit) of the slave address.
To write the data on the slave: sample 10-bit address- 101101101—
1. Master starts the communication by sending START bit on the bus. All connected slaves get alert that communication has been started.
2. The Master sends the address frame consists of 1111010 followed by “0” bit to write on the slave. All slaves connected to the bus listen to the 7-bit address and compare the last two bytes with their MSBs bytes of the address.
3. The address match slaves provide ACK say A1 to the Master. Remember, there can be more than one slave with the matched address.
4. After receiving a successful acknowledgement, the master sends second frame consist of another 8 bits of the slave address, say 11011010.
5. The remaining slaves (which provide ACK earlier) listen to this address and the matched address slave provides a successful ACK to the Master.
6. With successful ACK “A2” receive; the remaining process goes same as with 7-bit write addressing.
7. After writing the complete data, the slave sends the acknowledgement byte and the Master sends a STOP bit to terminate the communication.

Fig. 24: Image showing data format of I2C Communication for Master Device writing data to the Slave Device
To read the data from the slave: sample 10-bit address- 1011011010:
1. Master starts the communication by sending START bit on the bus. All connected slaves get alert that communication has been started.
2. The Master sends the address frame consists of 1111010 followed by “0” bit to write on the slave. All slaves connected to the bus listen to the 7-bit address and compare the last two bytes with their MSBs bytes of the address.
3. The address match slaves provide ACK say A1 to the Master.
4. After receiving a successful acknowledgement, the master sends the second frame consists of another 8 bits of the slave address, say 11011010.
5. The remaining slaves (which provide ACK earlier) listen to this address and the matched address slave provides a successful ACK to the Master and this slave remembers that it was addressed before.
6. Now, Master sends a repeated START byte and sends the first same frame “1111010” followed by “1” bit to read from the slave. Now, this slave then checks the frame and compares the 7-bits with the previous bits sent next after START byte and tests if the 8th bit is set to 1. If it matches, then the slave considers itself as a transmitter and sends a successful acknowledgement A.
7. The master then prepares itself to receive the data in the next frame from the slave.
8. After complete reception of data, Master sends a NACK bit to the slave to indicate that Master has completely fetched the data from the slave and it can stop sending it now.
9. Master then sends a STOP byte to terminate the communication.

Fig. 25: Image showing data format of I2C Communication for Master Device reading data from the Slave Device
Clock synchronization in Multi-Master Environment—We know that SDA data state changes only when the SCL clock signal is low and needs to be stable when the clock signal is high. In a multi-master mode, each master generates a clock on the SCL line, to maintain the data integrity on the SDA line, clock synchronization is needed on the SCL line. Clock synchronization is only needed when there are two or more than two masters.
If 2 masters generate clock at the same time then the synchronized SCL clock will be in LOW period till both masters put the clock in high state meaning if one master clock goes LOW for 200ms & then goes in HIGH state and other master goes LOW for 400ms then goes in high state, the complete LOW period for the SCL will be 400ms only and the master with shorter LOW clock period has to wait in HIGH state.
Similarly, the sync SCL clock will be in the HIGH period until the first master pulls it LOW. If any Master pulls the clock LOW first, the clock will be in the low state then. The SCL high period is determined by one of the shortest clock HIGH periods of Masters.
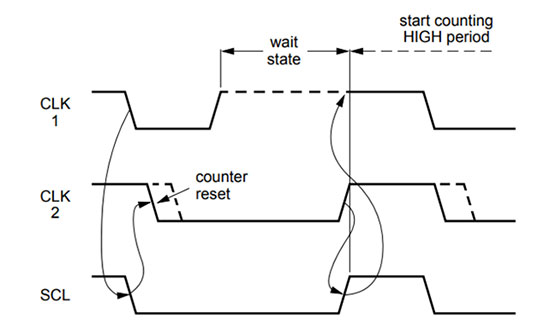
Fig. 26: Signal Diagram showing Clock Synchronization Process of I2C Communication
Arbitration Process—The arbitration process is also applied only where there is the multi-master environment. The way the clock synchronization has done, the data validity needs to be maintained. If two devices will send the data at a time then, there may be chances of losing the actual data. For this, the arbitration process is followed. The arbitration process is allowed on the master only; slaves are not involved in this process. It determines which master wins the race and continues sending the data over SDA line.
In the Arbitration procedure, after every bit sent on the SDA line, each master checks to see if the SDA line signal is the same as what it has sent on the line. If any master founds some mismatch with its bits like the SDA signal should be HIGH but it is LOW then it loses the race and other masters continue sending the data until one master wins the race.
No information is lost during the arbitration process and the master that loses the race may though generate the clock until the data sent completely and then restart its process again to win the race. Because they never lose hope ☺
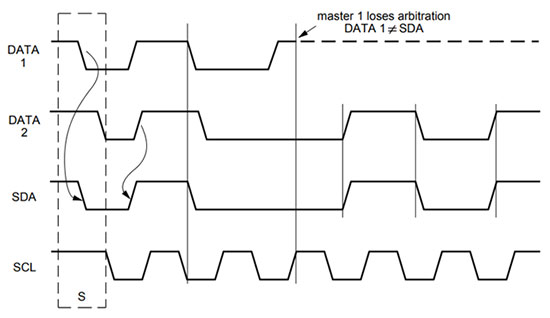
Fig. 27: Signal Diagram showing Arbitration Process between two Masters in I2C Communication
Clock Stretching—Clock stretching pauses the communication for some time and this is performed by slave only. We’ve studied that communication is mostly handled by master only but there is a case where slave isn’t able to handle the data or hasn’t processed the previous data yet, in that case, after master releases the SCL line HIGH, the Slave pulls it LOW until it is ready to receive the next data. After releasing the SCL line by a slave, the master controls the clock again.
§ Understand the Protocolfrom Developer End
So far, we have studied about the working of I2C Protocol; this is time to implement it on software with our hardware. The hardware setup for the protocol is very easy; connect the SDA and SCL line of the slave device (BMA250) to the SDA and SCL line of the master (Any microcontroller) and provide pull-up resistors on both the lines. We can take any value in between 4.7K to 10K, but for accuracy (it really matters in I2C Protocol), we should do some calculations. And make sure to connect their GND common.
Calculation of pull-up Resistor Rp—The value for the pull-up resistor depends on the bus capacitance. We calculate the minimum and maximum pull-up resistor for the bus. We can take a value between them.
Parameters to select for a pull-up resistor
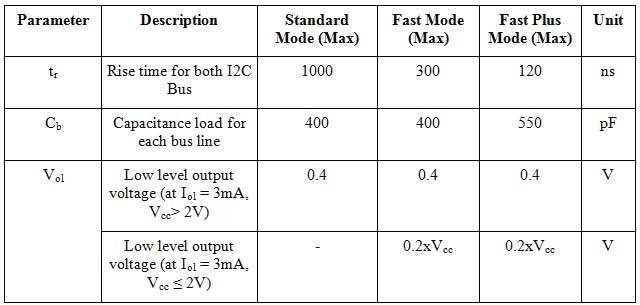
Fig. 28: Table listing parameters to select pull-up resistors for I2C Communication
Rp(min) =
where, VCC – power supply for the controller
Vol(max) – Low level output voltage
Iol – low level output current
Rp(max) =
We can calculate the resistance value using these formulas and can get an approximation value for our application. A strong pull-up resistor always prevents the I2C bus from being able to drive low.
Now, it’s time to implement in on software:
First step: Start with I2C Scanner
The first and easiest step is to scan the slave device at the master end, just to confirm our end device is working properly.
Arduino is really a great platform for electronics hobbyist and for professionals as well. If we are working with any controller architecture like AVR, ARM, PIC, 8051, we should first confirm our I2C device with the ArduinoI2C scanner code. This simple sketch shows all the I2C slave connected to the Master.
After checking with the scanner, we have found all our I2C devices connected. We are now confirmed that our hardware is working fine and our pull-up resistor values are correct. Next, we will implement our logic in the I2C frames.
Sample functions to see the I2C communication in C language
Note: The syntax used in this code, is taken for 8051 Controller. From these functions, we will understand the logic implementation only, for our controller, we will use the syntax accordingly.
/*
*This code snippet is provided us only to look over how I2C implement from the core.
*We can use these functions or can develop own functions using these functions.
*Enhancements: I2C blocking, 10-bit addressing, Arbitration etc.
*/
/*
* @fn DATA_LOW()
* brief this function is used to make the I2C data pin LOW
* we will use the syntax according to the controller and IDE to make the digital IO to LOW
* Input None
* Output None
* return None
*/
void DATA_LOW(void){
SDA_Pin= LOW;
//delay provide to hold the communication for given microseconds
halMcuWaitUs(5);
}
/*
* @fn DATA_HIGH()
* brief this function is used to make the I2C data pin HIGH
* we will use the syntax according to the controller and IDE to make the digital IO to HIGH
* Input None
* Output None
* return None
*/
void DATA_HIGH(void){
SDA_Pin= HIGH;
halMcuWaitUs(5);
}
/*
* @fn CLOCK_LOW()
* brief this function is used to make the I2C Clock pin LOW
* we will use the syntax according to the controller and IDE to make the digital IO to LOW
* Input None
* Output None
* return None
*/
void CLOCK_LOW(void){
SCL_Pin= LOW;
halMcuWaitUs(5);
}
/*
* @fn CLOCK_HIGH()
* brief this function is used to make the I2C Clock pin HIGH
* we will use the syntax according to the controller and IDE to make the digital IO to HIGH
* Input None
* Output None
* return None
*/
voidclock_HIGH(void){
SCL_Pin= HIGH;
halMcuWaitUs(5);
}
/*
* @fnI2C_wait()
* brief this function is used to hold the execution for 200 microseconds.
* Input None
* Output None
* return None
*/
staticvoidI2C_wait(void)
{
halMcuWaitUs(200);
}
/*
* @fnI2C_Start()
* @brief This function starts the I2C engine
* Input none
* Output none
* return none
*/
staticvoidI2C_Start(void)
{
DATA_HIGH();
I2C_wait();
CLOCK_HIGH();
I2C_wait();
DATA_LOW();
I2C_wait();
CLOCK_LOW();
I2C_wait();
}
/*
* @fnI2C_Stop()
* @brief this function stops the I2C engine
* Input none
* Output none
* return none
*/
staticvoidI2C_Stop(void)
{
DATA_LOW();
I2C_wait();
CLOCK_HIGH();
I2C_wait();
DATA_HIGH();
I2C_wait();
}
/*
* @fnI2C_ReStart()
* @brief This function restarts the I2C engine
* Input none
* Output none
* return none
*/
staticvoidI2C_ReStart(void)
{
DATA_HIGH();
CLOCK_HIGH();
I2C_Start();
}
/*
* @fnI2C_ReadBit()
* @brief this function reads the data from I2C bus bit by bit
* Input none
* Output none
* return acknowledgement
**************************************************/
static uint8 I2C_ReadBit(void)
{
uint8 ack;
DATA_HIGH();
I2C_wait();
CLOCK_HIGH();
I2C_wait();
if (!SCL_Pin){halMcuWaitMs(10); } //clock stretching
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
I2C_wait();
ack=SDA_Pin;
I2C_wait();
CLOCK_LOW();
I2C_wait();
returnack;//0=ack
}
/*
* @fnI2C_WriteBit()
* @brief this function writes the data on I2C bus bit by bit
* Input uint8
* Output none
* return none
**************************************************/
staticvoidI2C_WriteBit(uint8 value)
{
CLOCK_LOW();
I2C_wait();
if(value >0){
DATA_HIGH();
}
else{
DATA_LOW();
}
I2C_wait();
CLOCK_HIGH();
I2C_wait();
if (!SCL_Pin){halMcuWaitMs(10); } //clock stretching
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
if (!SCL_Pin){ halMcuWaitMs(10); }
I2C_wait();
CLOCK_LOW();
I2C_wait();
}
/*
* @fnI2C_SendByte()
* @brief this function sends the bytes of data through I2C protocol
* Input b
* Output none
* return ack
*/
static uint8 I2C_SendByte(uint8 b)
{
uint8 i;
uint8 ack;
for(i=0;i<8;i++){
I2C_WriteBit(b &0x80);
b =(b <<1);
}
ack=!(I2C_ReadBit());
returnack;//high = ACK received
}
/*
* @fnI2C_ReadByte()
* @brief this function reads the bytes of data through I2C protocol
* Input none
* Output none
* return byte
*/
static uint8 I2C_ReadByte(void)
{
uint8 byte =0;
uint8 i;
for(i=0;i<8;i++){
byte=(byte <<1)|I2C_ReadBit();
}
return byte;
}
A General Guidelinefor Its Protection
A series protection resistor can be added on the SDA and SCL lines to protect against high-voltage spikes or surges or ESD (Electrostatic discharge). The value of the resistor Rs should be small enough because it going to form a voltage divider with the pull-up resistor and will affect the voltage thresholds of the I2C signals. A value in between 33ohm-330ohm can be used.
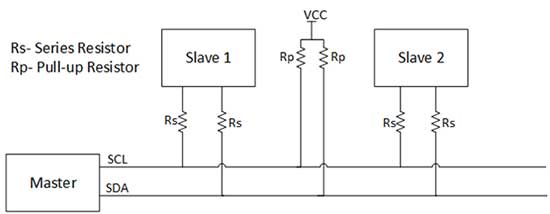
Fig. 29: Circuit Diagram of Protection technique for bus drivers
The Drawbackof Usingthe I2CBus
I2C can be used where we need less hardware space and synchronized data. But there are some major drawbacks of using I2C:
1. Implementing I2C protocol on software level required rich knowledge for the instruction sets used to configure and use the device.
2. It is a bit complex to set up because it requires device address to initialize and not so easy if our controller doesn’t have I2C support.
3. When comparing with SPI, I2C is a slow protocol.
4. Capacitance on the bus lines needs to be considered strictly otherwise chances of making garbage of the data.
If we have an adequate number of wires, then we can go for SPI protocol as well. ☺
You may also like:
Filed Under: Tutorials







Questions related to this article?
👉Ask and discuss on EDAboard.com and Electro-Tech-Online.com forums.
Tell Us What You Think!!
You must be logged in to post a comment.